Beispiel einer Kurvendiskussion
Gegeben sei eine Funktion $f$ mit $f(x)=3,5 x \cdot e^{(-0,6x)}$, die in der folgenden Abbildung zu sehen ist.
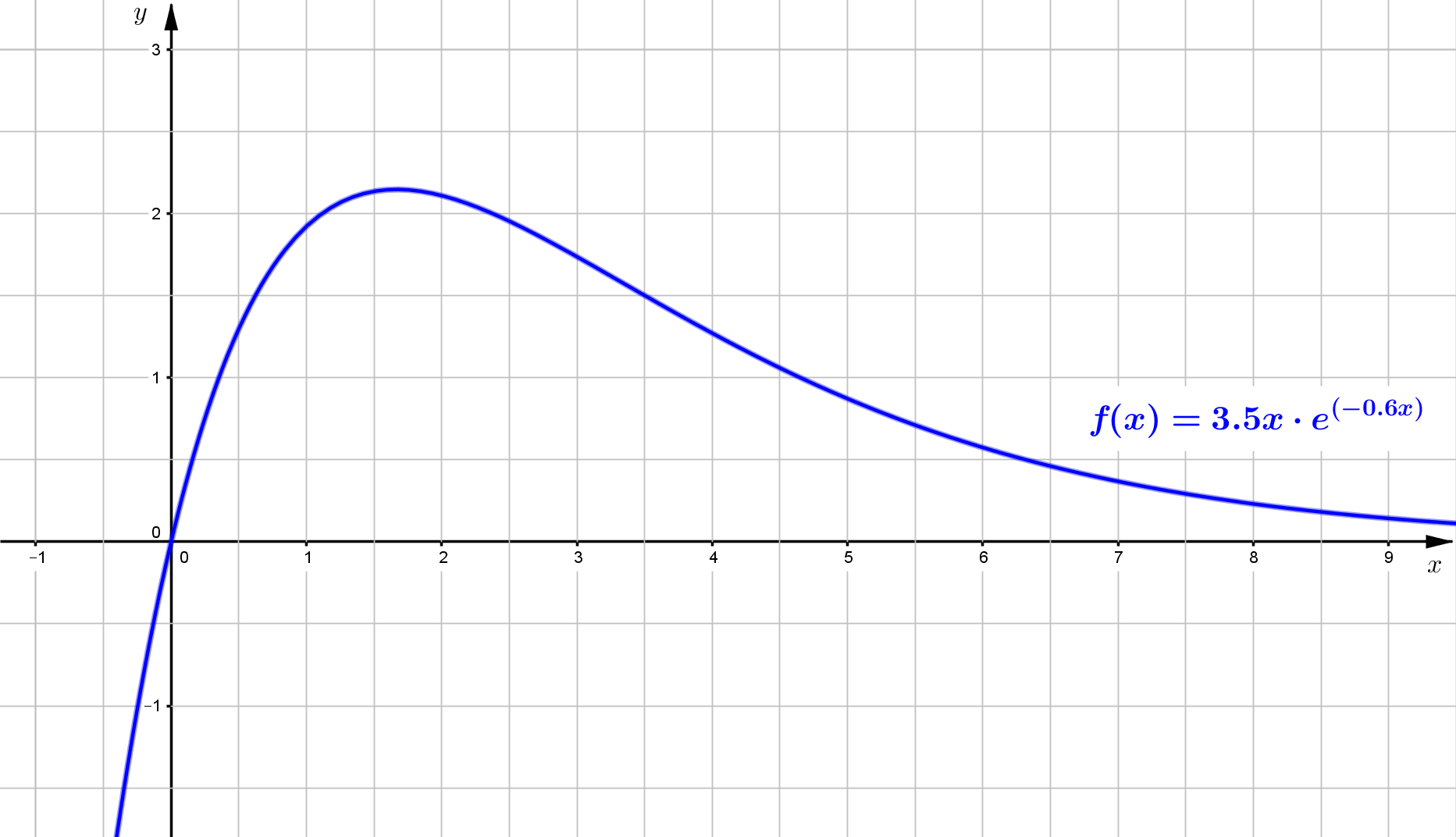
1. Globalverlauf
Zur Beschreibung des Globalverlaufs ist es notwendig, das Verhalten der Funktion für $x \rightarrow - \infty$ und für
$x \rightarrow \infty$ zu kennen. Für das Beispiel folgt damit:
\begin{align}
f(x \rightarrow - \infty) &\rightarrow - \infty \\
f(x \rightarrow \infty) &\rightarrow 0
\end{align}
Warum?
Für sehr große negative Werte von $x$ geht die $e$-Funktion gegen unendlich und $x$ geht gegen minus unendlich. Das Ergebnis muss also sein, dass die
Funktion insgesamt gegen minus unendlich strebt.
Für sehr große positive Werte von $x$ geht die $e$-Funktion gegen Null und $x$ geht gegen unendlich. Da die $e$-Funktion aber dominant ist gegen $x$,
geht die Funktion insgesamt gegen Null.
2. Symmetrien
Für die Betrachtung von Symmetrien vergleicht man die Funktion $f(x)$ mit $f(-x)$ (Achsensymmetrie) bzw. mit $- f(-x)$ (Punktsymmetrie). Hier:
\begin{align}
f(-x) &= 3,5 (-x) \cdot e^{(-0,6 (-x))} \\
f(-x) &= - 3,5 x \cdot e^{(0,6 x)} \not= 3,5 x \cdot e^{(-0,6 x)} \\ \\
f(-x) &\not= f(x)
\end{align}
Es ist damit keine Achsensymmetrie gegeben.
\begin{align}
- f(-x) &= - \left(-3,5 x \cdot e^{(0,6 x)} \right) \\
- f(-x) &= 3,5 x \cdot e^{(0,6 x)} \not= 3,5 x \cdot e^{(- 0,6 x)} \\ \\
- f(-x) &\not= f(x)
\end{align}
Punktsymmetrie liegt ebenfalls nicht vor.
3. Achsenschnittpunkte
1. $y$-Achse
Bedingung: $x = 0$
\begin{align}
f(0) &= 3,5 \cdot 0 \cdot e^{(-0,6 \cdot 0)} \\
f(0) &= 0
\end{align}
2. $x$-Achse (Nullstellen)
Bedingung: $f(x) = 0$
\begin{align}
3,5 x \cdot e^{(-0,6 x)} &= 0 \\
3,5 x = 0 &\lor e^{(-0,6 x)} = 0 \\
x &= 0
\end{align}
Für die $e$-Funktion gilt, dass sie für alle $x$-Werte positiv ist und nicht Null wird. Der Grenzwert für $x \rightarrow \infty$ ist
$e^{(- (x \rightarrow \infty))} \rightarrow 0$. Also gilt immer: $e^{(-x)} \not= 0$
Die einzige Nullstelle ist also $x_N = 0$.
4. Extrempunkte
Bedingung: $f'(x) = 0 \land f''(x) \gtrless 0$
Für die erste Ableitung wird die Produktregel benötigt, da in der Funktion zwei Faktoren vorkommen, die beide von $x$ abhängen. Es gilt also:
\begin{align}
f(x) &= u(x) \cdot v(x) \\ \\
u(x) = 3,5 x &\qquad v(x) = e^{(-0,6 x)} \\
u'(x) = 3,5 &\qquad v'(x) = -0,6 \cdot e^{(-0,6 x)} \\ \\
f'(x) &= u'(x) \cdot v(x) + v'(x) \cdot u(x) \\
f'(x) &= 3,5 \cdot e^{(-0,6 x)} + \left(-0,6 \right) \cdot e^{(-0,6 x)} \cdot 3,5 x \\
f'(x) &= e^{(-0,6 x)} \left( 3,5 - 0,6 \cdot 3,5 x \right) \\
f'(x) &= e^{(-0,6 x)} \left( 3,5 - 2,1 x \right)
\end{align}
Nach der ersten Bedingung folgt somit:
\begin{align}
e^{(-0,6 x)} \left( 3,5 - 2,1 x \right) &= 0 \\ \\
e^{(-0,6 x)} \not= 0 \land 3,5 - 2,1 x &= 0 \\
x &= \frac{3,5}{2,1} \\
x_E &= 1,67
\end{align}
Es gibt also eine Extremstelle bei $x = 1,67$.
Für die zweite Ableitung kommt wieder die Produktregel zur Anwendung:
\begin{align}
f'(x) &= u(x) \cdot v(x) \\ \\
u(x) = e^{(-0,6 x)} &\qquad v(x) = 3,5 - 2,1 x \\
u'(x) = -0,6 \cdot e^{(-0,6 x)} &\qquad v'(x) = -2,1 \\ \\
f''(x) &= u'(x) \cdot v(x) + v'(x) \cdot u(x) \\
f''(x) &= -0,6 \cdot e^{(-0,6 x)} \cdot \left(3,5 - 2,1 x \right) + \left(-2,1 \right) \cdot e^{(-0,6 x)} \\
f''(x) &= e^{(-0,6 x)} \left( -0,6 \cdot \left(3,5 - 2,1 x \right) - 2,1 \right) \\
f''(x) &= e^{(-0,6 x)} \left( -4,2 + 1,26 x \right)
\end{align}
Die zweite Bedingung liefert die folgende Gleichung:
\begin{align}
f''(x_E) &= e^{(- 0,6 \cdot 1,67)} \left( -4,2 + 1,26 \cdot 1,67 \right) \\
f''(x_E) &= -0,77 \lt 0 \qquad \rightarrow x_E \text{ ist ein Maximum}
\end{align}
$x_E$ eingesetzt in die Funktionsgleichung liefert den Funktionswert des Maximums:
\begin{align}
f(x_E) &= 3,5 \cdot 1,67 \cdot e^{(-0,6 \cdot 1,67)} \\
f(x_E) &= 2,15 \\ \\
\text{Max} \left( 1,67 / 2,15 \right)
\end{align}
5. Wendepunkte
Bedingung: $f''(x) = 0 \land f'''(x) \not= 0$
Aus der ersten Bedingung folgt:
\begin{align}
e^{(-0,6 x)} \left( -4,2 + 1,26 x \right) &= 0 \\ \\
e^{(-0,6 x)} \not= 0 \land -4,2 + 1,26 x &= 0 \\
x &= \frac{4,2}{1,26} \\
x_W &= 3,33
\end{align}
Die Wendestelle liegt bei $x = 3,33$.
Für die dritte Ableitung erhält man mit der Produktregel:
\begin{align}
f''(x) &= u(x) \cdot v(x) \\ \\
u(x) = e^{(-0,6 x)} &\qquad v(x) = -4,2 + 1,26 x \\
u'(x) = -0,6 \cdot e^{(-0,6 x)} &\qquad v'(x) = 1,26 \\ \\
f'''(x) &= u'(x) \cdot v(x) + v'(x) \cdot u(x) \\
f'''(x) &= -0,6 \cdot e^{(-0,6 x)} \cdot \left(-4,2 + 1,26 x \right) + 1,26 \cdot e^{(-0,6 x)} \\
f'''(x) &= e^{(-0,6 x)} \cdot \left( \left( -0,6 \right) \cdot \left(-4,2 + 1,26 x \right) + 1,26 \right) \\
f'''(x) &= e^{(-0,6 x)} \left( 3,78 - 0,756 x \right)
\end{align}
Aus der zweiten Bedingung folgt damit:
\begin{align}
f'''(x_W) &= e^{(-0,6 \cdot 3,33)} \left( 3,78 - 0,756 \cdot 3,33 \right) \\
f'''(x_W) &= 0,17 \not= 0 \qquad \rightarrow x_W \text{ ist eine Wendestelle}
\end{align}
Einsetzen in die Funktionsgleichung liefert den Funktionswert des Wendepunktes:
\begin{align}
f(x_E) &= 3,5 \cdot 3,33 \cdot e^{(-0,6 \cdot 3,33)} \\
f(x_E) &= 1,58 \\ \\
\text{W} \left( 3,33 / 1,58 \right)
\end{align}
Aufgrund dieser Angaben (Globalverlauf, Achsenschnittpunkte, Extrema und Wendepunkte) kann der Graph der Funktion skizziert werden:




